二阶高通滤波器性能解析


一、传递函数推导(核心内容)
运用节点电流法,可以精准求解出该二阶高通滤波器的传递函数。
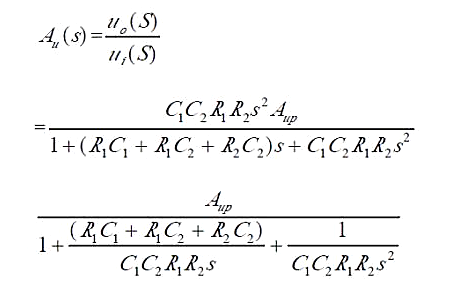
该方法通过对电路中各节点电流的分析,建立相应的数学方程组,进而求解出输出与输入之间的关系表达式。具体而言,通过对滤波器电路中关键节点的电流进行分析,综合考虑各电路元件的特性,如电阻、电容等对电流的影响,最终推导得到传递函数的表达形式。该传递函数能够清晰地反映出滤波器在不同频率下的响应特性。
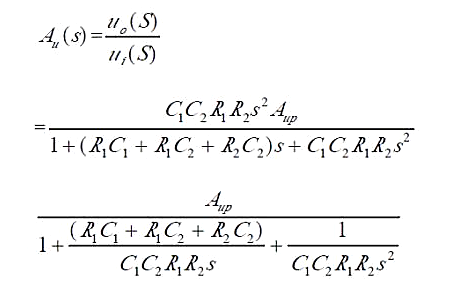
该方法通过对电路中各节点电流的分析,建立相应的数学方程组,进而求解出输出与输入之间的关系表达式。具体而言,通过对滤波器电路中关键节点的电流进行分析,综合考虑各电路元件的特性,如电阻、电容等对电流的影响,最终推导得到传递函数的表达形式。该传递函数能够清晰地反映出滤波器在不同频率下的响应特性。
二、频率特性(核心内容)


二阶有源高通滤波器的电路仿真图如下:
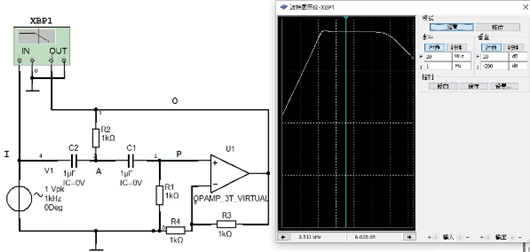

当R1=R2=R,C1=C2=C时,其传递函数具有特定的形式,能够体现出明显的高通特性。
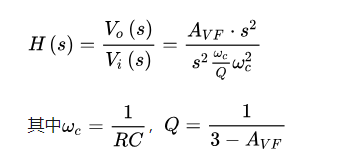
从传递函数的表达式可以深入分析其频率特性:当频率较低时,即s值很小时,Vo(s)/Vi(s)的比值也很小,表明滤波器对低频信号具有很强的衰减作用;随着频率的升高,s值增大,Vo(s)/Vi(s)的比值也随之增大,意味着滤波器逐渐允许高频信号通过;当s接近于无穷时,Vo(s)/Vi(s)的比值趋于最大值AVF,体现了滤波器在高频段的稳定增益。
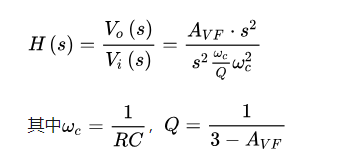
从传递函数的表达式可以深入分析其频率特性:当频率较低时,即s值很小时,Vo(s)/Vi(s)的比值也很小,表明滤波器对低频信号具有很强的衰减作用;随着频率的升高,s值增大,Vo(s)/Vi(s)的比值也随之增大,意味着滤波器逐渐允许高频信号通过;当s接近于无穷时,Vo(s)/Vi(s)的比值趋于最大值AVF,体现了滤波器在高频段的稳定增益。
在仿真图中,波特图能够直观地展示滤波器的频率响应特性。在低频区间,增益很小,有效抑制了低频噪声和干扰;而在高频区间,增益达到一个近似定值,确保高频信号能够稳定传输。然而,需要注意的是,在频率特别高的情况下,由于实际运算放大器(运放)的带宽有限,增益会出现一定程度的下降。这是因为运放的频率响应特性限制了其在极高频率下的性能表现。因此,在实际应用中,选用运放时必须确保其带宽足够能够通过所有的有效信号,以保障滤波器在整个工作频段内的性能稳定性和可靠性。
〈烜芯微/XXW〉专业制造二极管,三极管,MOS管,桥堆等,20年,工厂直销省20%,上万家电路电器生产企业选用,专业的工程师帮您稳定好每一批产品,如果您有遇到什么需要帮助解决的,可以直接联系下方的联系号码或加QQ/微信,由我们的销售经理给您精准的报价以及产品介绍
联系号码:18923864027(同微信)
QQ:709211280


